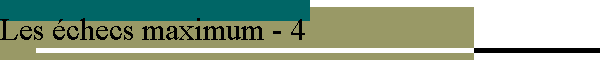Encore un problème difficile à résoudre, car la solution implique un trajet très précis de la tour blanche. De plus, on ne voit pas très bien comment les noirs pourraient mater le roi blanc (mat inverse) alors que celui-ci dispose de 3 cases de fuite. Enfin, et c'est peut-être l'énigme la plus difficile à résoudre, comment empêcher le fou d'osciller sur la diagonale a3-f8 (longueur 7,07) ? En interposant la tour blanche sur cette diagonale me direz-vous. Oui, mais dans ce cas, c'est la tour noire h8 qui prendrait le relais, en oscillant sur la rangée a8-h8 (longueur 7) !
Meynsbrughen Michel
Inédit
Mat en 7 coups
Maximum inverse
Quelques idées qui ne mènent à rien :
1.Cg3, Ff8 2.Tc6, Fa3 3.Tc2+, Rxg3 4.Tg2+, hxg2+ 5.Rg1, Ff8 6.??? le pion e5 est bien démuni...
1.Cf2, Ff8 2.Cd3, Fa3 3.Tc6, Ff8 4.Tc2+, Rg3 5.Tg2+, hxg2+ 6.Rg1, Fa3 7.Cb4, Ta8 ! (les noirs ayant le choix entre 2 coups de longueur égale (Ta8 ou Th1 mat) choissent le coup le moins favorable aux blancs).
Tableau des distances :
Déplacement de n cases
1
2
3
4
5
6
7
Exemples de longueurs de coups
Orthogonal (x1)
Ra1-a2=1 Tb5-d5=2 Dd1-d8=7
Diagonal (x racine de 2)
1,41
2,83
4,24
5,66
7,07
8,48
9,90
Ra1-b2=1,41 Fd7-f5=2,83 Dh8-e5=4,24
Cavalier (=racine de 5)
2,24
Cc8-a7=2,24